Convariance 공분산

1. 정의

Covariance는 한국말로는 공분산이라고 할 수 있고, 보통 Cov 라고 표현한다.
공분산은 두 개 또는 그 이상의 랜덤 변수에 대한 의존성을 의미한다.

2. 의존성

1. 개요

어떤 특정 샘플의 X라는 특징이 x의 평균 보다 크고, 그 샘플의 Y라는 특징이 y의 평균 보다 크다면, 각각의 편차는 둘 다 양수가 된다. 그 말은 X가 큰 값을 가질 때 Y도 큰 값을 가진다는 의존성을 보여준다.
이러한 경향이 크게 나타난다면, 자연스럽게 반대 방향도 함께 일어난다. 반대 방향이라는 것은 X가 작은 값을 가질 때는 자연스럽게 Y의 작은 값이 된다. 이 때에도 마찬가지로 편차의 곱은 양수가 된다. 왜냐하면 "음수 x 음수 = 양수" 이기 때문이다. 이러한 상태에서 평균을 취하게 되면 큰 양수 값이 나오게 된다.
즉, 정의에 의해서 X가 증가할 때, Y도 증가하려고 하고, X가 감소할 때, Y도 감소하려고 하는 모습을 보이기 때문에 X와 Y 사이의 의존성이 높다고 할 수 있다.

2. 선형관계

가장 의존성이 낮은 상황은 당연히 서로 독립인 상황이다. X가 어떻게 되든 상관 없이 Y는 어떤 값이든 가질 수 있다. 즉, X가 높은 값을 가졌을 때, Y는 높은 값일 수도 있고, 아닐 수도 있다. 그것이 완전히 랜덤이라면, 편차의 곱 항이 양수와 음수가 골고루 나올 것이고, 그걸 평균하면 0에 가까울 것이다.
표기하기로는 Cov(X, Y)라고 주로 하지만, 시그마를 사용해서 index로 변수 두 개를 넣어서 하기도 한다. 분산은 한 변수에 대해서 Cov(X, X)를 한 거랑 마찬가지이고, 따라서, 제곱의 형태가 되기 때문에 분산은 항상 양수가 되어야 한다. 하지만 앞에서 설명했듯이 Cov는 양수도 음수도 될 수 있다. 이러한 상황을 선형 관계라고한다. XY를 곱한 것의 평균이 공분산이 될 수 있다.

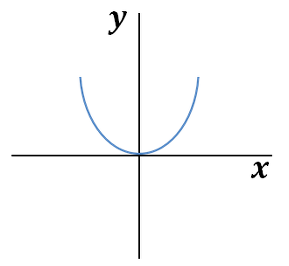
하지만, 공분산이 0이라고 해서 항상 독립이 되진 않는다. 이유는 공분산은 선형 관계에 대한 의존성을 말하고, 공분산이 0이 되면 두 변수의 선형 관계가 없다는 것을 의미하지, 모든 관계가 없다는 것을 의미하진 않기 때문이다. 독립이라는 조건은 두 변수의 모든 관계가 없다는 것을 의미하므로, 그냥 독립이라는 개념이 보다 상위 개념이 된다. 즉, y = x^2 이라는 관계가 있고, 그래프로 표현하면 위와 같다고 한다면, 여기서 y와 x는 서로 선형이 아니기 때문에 cov(x,y) = 0이 된다.
하지만, 그렇다고 이 두 변수가 독립이라고는 할 수 없다. 이유는 x가 0에서부터 증가하면 y가 증가하고, x가 0에서부터 감소하면 y가 또 증가하는 이러한 관계를 가지기 때문이다.

3. 요약

공분산은 서로 다른 변수들 사이에 얼마나 의존하는지를 수치적으로 표현하며, 그것의 직관적 의미는 어떤 변수(X)가 평균으로부터 증가 또는 감소라는 경향을 보일 때, 이러한 경향을 다른 변수(Y 또는 Z 등등)가 따라 하는 정도를 수치화 한 것이다. (공분산은 또한 두 변수의 선형 관계의 관련성을 측정한다라고도 할 수 있다.)

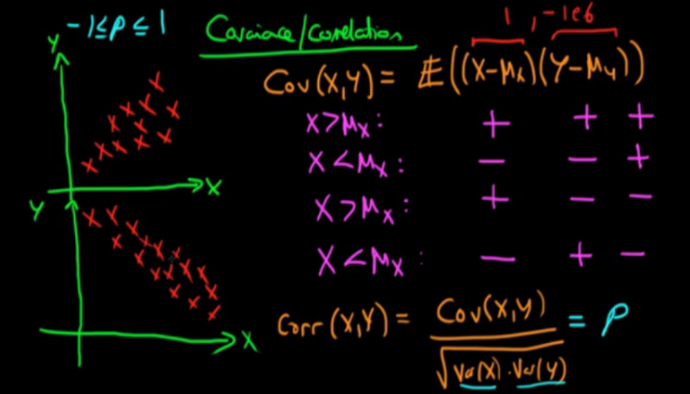
이러한 현상을 잘 정리한 그림이 있어서 참조하였다. 여기에는 Correlation에 대한 설명도 함께 하는데 Corr(X,Y)는 -1부터 1까지의 값을 가지며, -1일 때는 가장 Negative 의존성이 높은 상태이며, +1이면 가장 Positive 의존성이 높은 상태이고 0일 때는 의존성이 없는 상태이다.

3. 참조

https://blog.naver.com/sw4r/221025662499