L1L2

1. Diffrence Norm

Norm은 벡터의 크기(혹은 길이)를 측정하는 방법(혹은 함수)이다. 두 벡터 사이의 거리를 측정하는 방법이기도 하다.

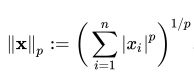
＊p = 1 이면 L1 Norm, P = 2 이면 L2 Norm.
＊n은 해당 벡터의 원소 수

1. L1 Norm

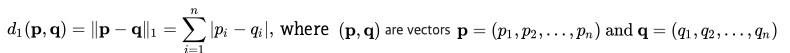
L1 Norm 은 벡터 p, q 의 각 원소들의 차이의 절대값의 합이다. 예를 들어 벡터 p =(4, 1, -2), q = (5, 0, 7) 이라면 p, q의 L1 Norm 은 |4-5| + |1-0| + |-2 -7| = 1 + 1 + 9 = 11 이다

2. L2 Norm

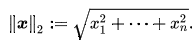
L2 Norm 은 벡터 p, q 의 유클리디안 거리(직선 거리)다. 여기서 q 가 원점이라면 벡터 p, q의 L2 Norm 은 벡터 p 의 원점으로부터의 직선거리다.

이러한 특성 때문에 L2 Norm은 오직 두 점사이의 직선으로만 표현될 수 있지만 두 점사이의 거리를 표현하는데 비교적 다양한 방식으로 표현될 수 있다.

2. Difference Loss

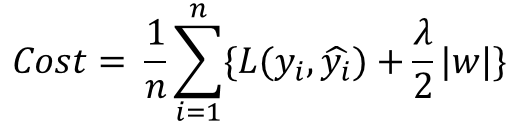
y_i 는 실제 값을, f(x_i)는 예측치를 의미한다. 실제 값과 예측치 사이의 오차 값의 절대값을 구하고 그 오차들의 합을 L1 Loss 라고 한다.

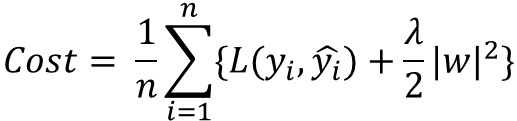
L2 Loss는 오차의 제곱의 합으로 정의된다.

L2 Loss는 오차의 제곱을 더하기 때문에 Outlier에 더 큰 영향을 받는다. 즉 L1 Loss가 Outlier에 둔감하다라고 표현할 수 있다.

Outlier가 적당히 무시하는 방향이면 L1 Loss, 많이 신경을 써야하면 L2 Loss를 사용하는 것이 대중적이다.

주의할 점은 L1 Loss는 0인 지점에서는 미분이 불가능하다.

3. Diffrence Regularization

Regularization(일반화)는 Overfitting을 예방하고 Generalization 성능을 높이는데 도움을 주는 방법이다. L1 Regularization, L2 Regularization, Dropout 등이 있다.

model이 overfitting으로 진행되는 원인 중 하나는 cost값이 작아지는 과정에서 특정 weight값이 너무 커지기 때문에 일반화가 힘들어지는 것이다.

위 수식은 L1 Regularization을 표현한 것인데, 가장 중요한 것은 cost function에 weight의 절대값을 더해준다는 것이다. 기존 함수에 수식이 사용되면서 weight값이 너무 크지 않은 방향으로 학습되도록 한다.

위 수식은 L2 Regularization을 표현한 것인데, weight의 제곱을 더하여 값이 너무 커지지 않도록 학습되게 한다.

벡터 p,q의 값을 p = (0.3, -0.3, 0.4), q = (0.5, -0.5, 0)로 가정한다.
L1 Norm으로 계산하면 수식은 아래와 같다.
|0.3| + |-0.3| + |0.4| = 1
|0.5| + |-0.5| + |0| = 1

L2 Norm으로 계산하면 결과는 각각 0.583095, 0.707107이다.

위 수식의 결과로 L2 Norm은 각각의 벡터에 관해서 항상 특정한 결과를 출력한다. 하지만 L1 Norm은 경우데 따라 특정 요소가 달라도 같은 결과를 나타낼 수 있다. 즉, L1 Norm은 Feature Selection이 가능하고 Sparse Model에 적합하다. 이러한 특징 때문에 convex optimization에 유용하게 쓰인다.